Unity和Android的相互的调用
本文共 321 字,大约阅读时间需要 1 分钟。
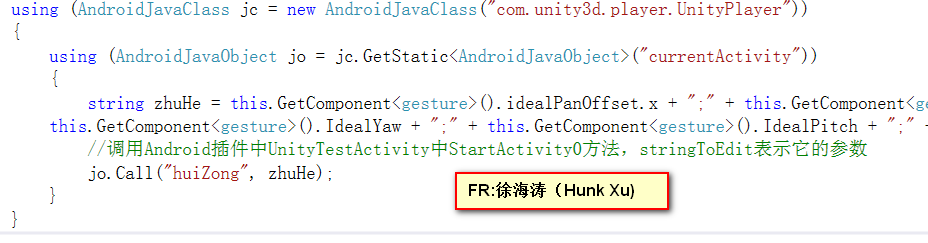
1 unity调用Android,注意jc和jo要用using包起来,否则可能会闪退
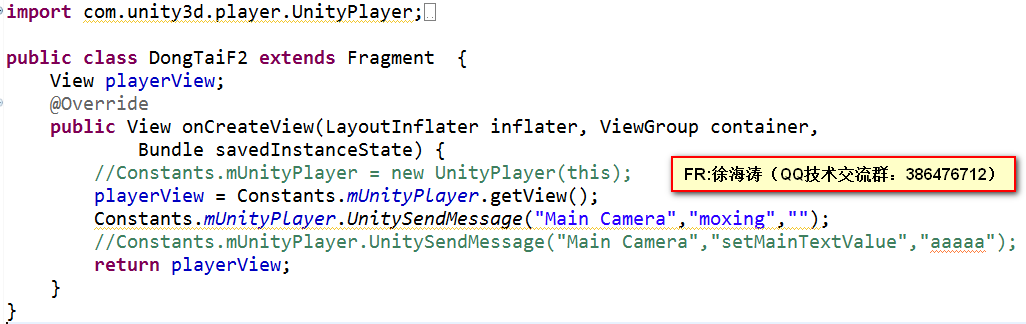
2 Android调Unity,Android中我使用的是碎片
public void tiaoToAndroid() { AndroidJavaClass jc = new AndroidJavaClass("com.unity3d.player.UnityPlayer"); AndroidJavaObject jo = jc.GetStatic ("currentActivity"); jo.Call("diaoYongMoJing"); } FR:徐海涛(Hunk Xu)
你可能感兴趣的文章